Thrifty query execution via incrementability
[1] 是另一篇关于物化视图维护的维护计划的研究工作。但和之前的工作 [2] 不同的是,[1] 没有考虑对不同的输入采取不同的维护计划,而是对一个视图中的不同算子使用不同的维护计划。[1] 分析了不同算子的增量计算能力,使用动态规划给出了一个视图维护的维护计划。
问题定义
物化视图可以通过一个查询语法树来表示。在这个查询语法树中,我们有多个查询路径(query path),每个查询路径由输入、输出和一系列算子组成。下图就是一个具有多个查询路径的视图的示例。
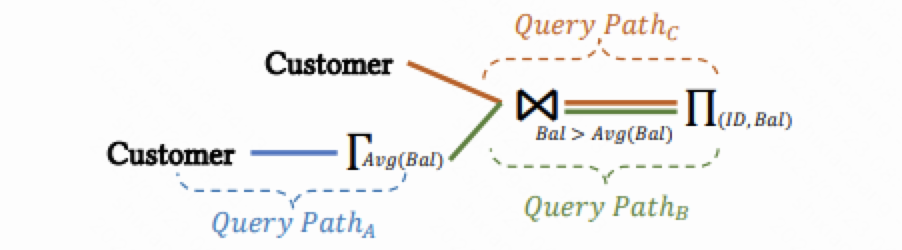
在查询路径上,会有一些堵塞算子(blocking operators),如排序、聚合和distinct等。每个堵塞算子都有一个输出缓存,将自己的计算结果保存在这个缓存中。当缓存中的数据到达一定阈值时,下游的算子就会被调度执行来清空缓存中的数据。
每个算子可以使用不同的调度频率来情况输出缓存。为了简化设定,论文按照输入数据量占全部数据量的比例来清空缓存。当调度频率为$k$时,算子在收到全部数据量的$1/k$时被调度执行,并清空其对应的缓存。$k$越大,则意味着算子有更高的调度频率;而当$k=1$时,则意味着算子只有在输入完全到达时才会被执行。
如果一个物化视图的查询树中存在$Q$个查询路径,那么这个物化视图的维护计划可以用这$Q$个查询路径的缓存清空策略来表示。我们使用数组$P = (P_1, P_2, …, P_Q)$表示物化视图的维护计划,其中$P_i$表示第$i$个查询路径的缓存清空策略。注意到,每个算子的调度频率不可能高于输入算子的调度频率,因此对所有的$j \in \text{children}(i)$, $P_i \le P_j$,其中$\text{children}(i)$返回在查询路径中算子$i$的所有下游算子。
对于一个维护计划$P$,我们使用$\mathcal{C}_F(P)$表示在最终查询时需要花费的开销,$\mathcal{C}_T(P)$表示维护和查询的花销。通过更加频繁的维护,我们可以减少最终查询时的开销,但也会增加系统整体的开销。我们希望在满足查询开销在一定阈值的情况下,尽可能减少整体的开销。因此我们的问题可以抽象为
$$
\begin{aligned}
& \text{minimize} &\mathcal{C}_T(P) \\
& \text{subject to} &\mathcal{C}_F(P) \le L \times \mathcal{C}_F(\bar{P})
\end{aligned}
$$
其中$\bar{P}=(1, 1, …, 1)$,表示视图按照完全批式的方式计算,即所有的算子都只在上游的数据完全到达之后才开始进行计算;$L$是一个设定的阈值。
计算增量收益
对任意两个维护计划$P_1$和$P_2$,如果$P_2$中所有查询路径的调度频率都不小于$P_1$中对应查询路径的调度频率,我们则称$P_2 \ge P_1$。
如果一个维护计划能够通过更高的调度频率减少更多的查询开销,那么我们就认为这个维护计划具有更好的增量计算能力。给定两个维护计划$P_1$和$P_2$,$P_2 > P_1$,我们通过下面这个公式来计算$P_2$相比于$P_1$通过增量计算获得的收益:
$$Inc(P_1, P_2) = \frac{\mathcal{C}_F(P_1) - \mathcal{C}_F(P_2)}{\mathcal{C}_T(P_2) - \mathcal{C}_T(P_1)}$$
基于上面的公式,我们进一步可以用$Inc(P) = Inc(P, \bar{P})$得到任意一个维护计划$P$的增量收益。如果$Inc(P) = \infty$,则意味着这个视图可以充分的通过增量计算进行维护,每当更新到达时就立即对视图进行维护,从而在查询不需要再花费任何的开销;而如果$Inc(P) = 0$,那么这个视图无法通过提前的增量计算减少最终查询的开销,我们只需要在必要的时候对视图进行维护即可。
寻找维护计划
论文设计了一个贪心算法来利用增量收益减少搜索空间。
| 0 | $P \gets \bar{P}$ |
| 1 | while true do |
| 2 | $i \gets \text{argmax}_{i: P_i < P_j, \forall j \in \text{children}(i)} \partial_i(P)$ |
| 3 | if $\partial_i (P) \le 0$ then |
| 4 | return P |
| 5 | end if |
| 6 | $P[i] \gets P[i] + 1$ |
| 7 | if $\mathcal{C}_F(P) \le L \times \mathcal{C}_F(\bar{P})$ then |
| 8 | return $P$ |
| 9 | end if |
| 10 | end while |
我们从完全批量计算的维护计划$\bar{P}$开始,依次增加查询路径的调度频率。在每次调整时,我们遍历所有的查询路径,寻找能够带来最大增量收益的查询路径,并将其对应的调度频率加一。当维护计划可以满足查询开销的约束时,我们就立即返回。
小结
这个工作提供物化视图的维护调度中另一个维度的视角,考虑对数据链路上的不同算子采取不同调度来优化整体的维护开销。这个论文花费了较大的精力来对维护计划的开销进行评估,包括考虑不同更新类型的基数估计等。但在最终维护计划的搜索上,论文使用了一个简单的贪心算法。由于论文选择从最差的计划开始贪心,所以感觉这个贪心算法很难有机会得到一个最优的维护计划。
参考文献
[1] D. Tang et al. Thrifty query execution via incrementability. In SIGMOD 2020, pp. 1241-1256.
[2] H. He et al. Asymmetric batch incremental view maintenance. In ICDE 2005, pp. 106-117.
Thrifty query execution via incrementability